Notación BigO
Me he topado con entrevistas de trabajo sobre todo en Oracle, en las que hacen hincapié en el tema de la O grande o comúnmente conocida como BigO.
"La Notación BigO es la representación relativa de la complejidad de un algoritmo"
¿Cuál es el tiempo de complejidad de tu algoritmo?
¿Puedes mejorar el tiempo de complejidad de tu algoritmo?
Dos preguntas cruciales en las entrevistas de trabajo, las cuales podrás resolver a continuación.
Representación: Simplificar la comparación de algoritmos en una sola variable.
Relativa: Comparación entre algoritmos similares.
Complejidad: Comportamiento del algoritmo cuando la entrada de datos aumenta. ¿Más memoria? ¿Más tiempo?
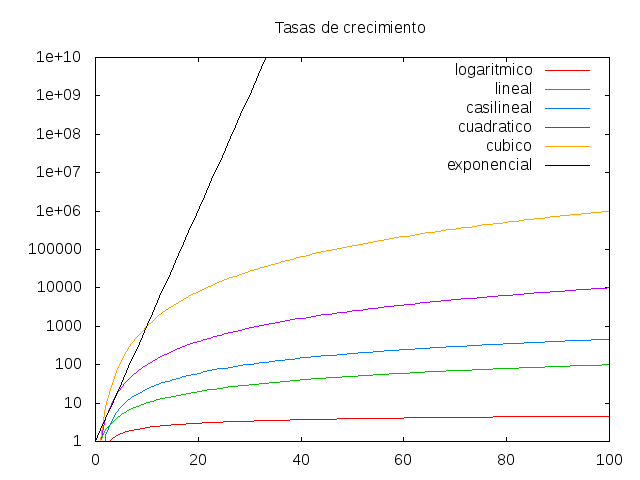
Existen varios tipos de complejidades, pero enlisto sólo las más comunes.
- Complejidad Constante O(1)
- Complejidad Logarítmica O(log n)
- Complejidad Lineal O(n)
- Complejidad Lineal-Logaritmica O(n log n)
- Complejidad Cuadrática O(n2)
Donde n significa el número de datos a procesar.
Complejidad Constante O(1): Cantidad de datos es irrelevante, es decir, tardará el mismo tiempo en ejecutarse el algoritmo.
Ejemplos complejidad O(1) "Declaraciones simples"
Solo es una linea y para todos ellos la complejidad es constante.
int a=0;
a=5;
a++;
Ejemplos:
- Acceder al elemento de un arreglo
- Insertar un elemento en una lista ligada
- Añadir o sacar un elemento de una pila
Complejidad Logarítmica O(log n): El tiempo incrementa conforme aumenta el número de elementos, pero logarítmicamente, es decir, es muy corto tiempo.
Recordemos que el log es la inversa de la exponencial
Para esto:
Ejemplo complejidad O(log n) "Divide y vencerás"
Buscar el mayor número de un arreglo [3,5,6,4,10], podemos ver que tenemos la opción mas sencilla a simple vista: recorrer todo el arreglo N=5.
Por lo tanto la complejidad seria O(N) o bien O(5)
¿Pero si en lugar de 5 fueran 130 elementos? Sería mayor el número de operaciones.
Realizar un algoritmo con complejidad O(log(n)) sería la mejor opción, es decir log130 sería un poco más de 7 (siete operaciones que se realizarían).
La búsqueda binaria es el ejemplo más sencillo para entender esta complejidad.
1.- Ordenar arreglo
2.- Dividir en dos partes el arreglo e ir buscando sólo en la parte que contenga más próximo al número buscado, esto reducirá a 7 operaciones únicamente.
Ejemplos:
- Búsqueda binaria.
- Encontrar el may-men elemento en un árbol de búsqueda binaria
- Algoritmo "Divide y vencerás"
Complejidad Lineal O(n): Cuán más grande sea la cantidad de datos, el tiempo de respuesta aumentará proporcionalmente.
Ejemplos complejidad O(n) "Ciclos sencillos"
El ciclo se iterará n veces
for(int i=0;i<n;i++)
{
//declaraciones simples
}
Complejidad: O(n)
Ejemplos:
- Recorrer un arreglo o lista ligada
- Búsqueda lineal
- Comparar dos cadenas
Complejidad Lineal-Logarítmica O(n log n): Combinación de la lineal y la logarítmica, es común encontrarnos algoritmos de ordenamiento para esta categoría.
Ejemplos:
- Merge Sort
- Heap Sort
- Quick Sort
Ejemplo: Bucles donde la evolución de la variable de control no es lineal, junto a bucles con variable lineal.
int c, x; //O(1)
for (int i=0;i<n;i++) { //O(n) variable de control lineal
c=i;// O(1)
while(c > 0) //O(log n) variable de control no lineal
{
x = x % c; //O(1)
c = c / 2; //O(1)
}
x+=2; //O(1)
}
Complejidad: O(1) * O(n) * O(log n) = O(n log n)
Complejidad Cuadrática O(n2): El tiempo se dispara rápidamente, no es muy eficiente al tratarse de una gran cantidad de datos.
Ejemplos complejidad O(n2) "Ciclos anidados"
Se multiplica la complejidad exterior con la interior; n es el número de veces que se ejecutará el ciclo.
for(int i=0;i<n;i++) O(n)
{
for(int j=0;j<n;j++) O(n)
{
//declaraciones simples
}
}
=O(n*n) = O(n2)
Ejemplos:
- Bubble Sort
- Selection Sort
- Iterar un arreglo de dos dimensiones
Sin Embargo...
¿Qué pasa si nuestro algoritmo no presenta ninguna de las categorías anteriores?
Ejemplo: O(n+3)
Sólo nos interesaría O(n) ya que conforme aumente n, la constante 3 sería insignificante.
Ejemplo: O(n2 +2n +3)
Sólo se toma O(n2) siendo la potencia más grande.
Cuando se analiza un algoritmo existen 3 diferentes casos:
- Best Case
- Average Case
- Worst Case
Wors Case, es el más representativo ya que nos indica la categoría de complejidad más alta. Por ejemplo un algoritmo de búsqueda lineal tiene complejidad O(n):
- Worst Case: Recorrer todo el arreglo O(n)
- Average Case: Recorrer la mitad de los elementos O(n/2)
- Best Case: Primer elemento es el buscado O(1)
Es muy importante analizar la complejidad de un algoritmo, ya que normalmente lo hacemos sólo con poca o mediana cantidad de datos que puede culminar en un tiempo aceptable, pero no estamos seguros si funcionará con una enorme cantidad de datos (millones).
Ejemplos:
1.- Cuál es el tiempo y complejidad de espacio del siguiente código: int a = 0, b = 0; //O(1)
for (i = 0; i < N; i++) { //O(N)
a = a + rand(); //O(1)
}
for (j = 0; j < M; j++) { //O(M)
b = b + rand(); //O(1)
}
Se suman las 3. pero como en O(1) 1 es una constante.
Asume que rand() es O(1).2.- Cuál es el tiempo y complejidad de espacio del siguiente código:
int a = 0, b = 0; //O(1)
for (i = 0; i < N; i++) { //O(N)
for (j = 0; j < N; j++) { //O(N)
a = a + j;
}
}
for (k = 0; k < N; k++) { //O(N)
b = b + k;
}
Los ciclos anidados representan O(N*N) más el segundo ciclo O(N), el espacio de complejidad sería O(1). Así bien, como O(N*N) + O(N), pero como O(N) sería insignificante comparándolo con O(N*N), sólo se deja este ultimo termino.
3.- ¿Cuál es la complejidad del siguiente código?
int a = 0, i = N;
while (i > 0) {
a += i;
i /= 2;
}
En cada iteración podemos ver que i se convierte en i/2, en cada iteración i sería la mitad del valor de N.
4.- ¿Cuál es la complejidad del siguiente código?
int a = 0;
for (i = 0; i < N; i++) { //O(N)
for (j = N; j > i; j--) { //O(N)
a = a + i + j;
}
}
Como son ciclos anidados: O(N*N)




